StackOverflow1: The lower the loss, the better a model (unless the model has over-fitted to the training data). The loss is calculated on training and validation and its interperation is how well the model is doing for these two sets. Unlike accuracy, loss is not a percentage. It is a summation of the errors made for each example in training or validation sets.
In the case of neural networks, the loss is usually negative log-likelihood and residual sum of squares for classification and regression respectively. Then naturally, the main objective in a learning model is to reduce (minimize) the loss function’s value with respect to the model’s parameters by changing the weight vector values through different optimization methods, such as backpropagation in neural networks.
Loss
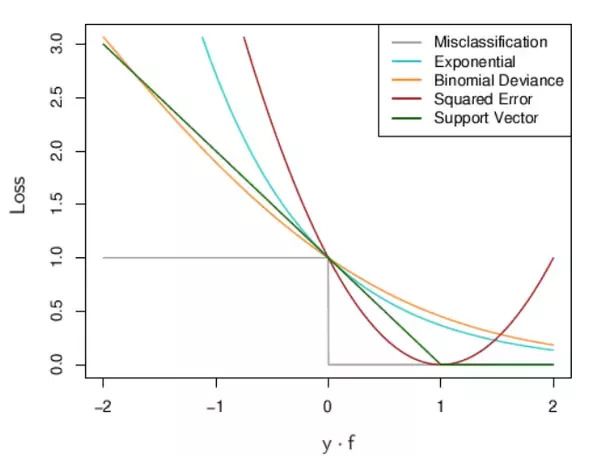
Loss value implies how well or poorly a certain model behaves after each iteration of optimization. Ideally, one would expect the reduction of loss after each, or several, iteration(s).
The accuracy of a model is usually determined after the model parameters are learned and fixed and no learning is taking place. Then the test samples are fed to the model and the number of mistakes (zero-one loss) the model makes are recorded, after comparison to the true targets. Then the percentage of misclassification is calculated.
For example, if the number of test samples is 1000 and model classifies 952 of those correctly, then the model’s accuracy is 95.2%.
There are also some subtleties while reducing the loss value. For instance, you may run into the problem of over-fitting in which the model “memorizes” the training examples and becomes kind of ineffective for the test set. Over-fitting also occurs in cases where you do not employ a regularization, you have a very complex model (the number of free parameters W is large) or the number of data points N is very low.
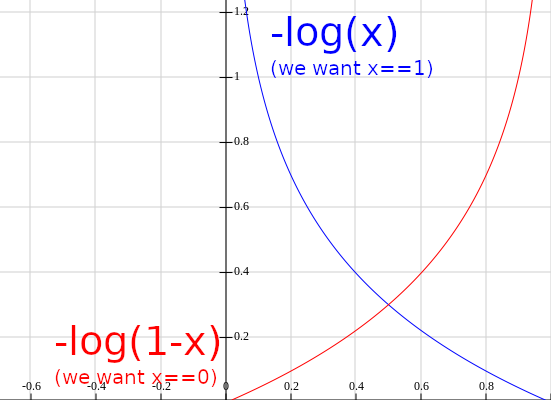
Negative Log-Likelihood (NLL)
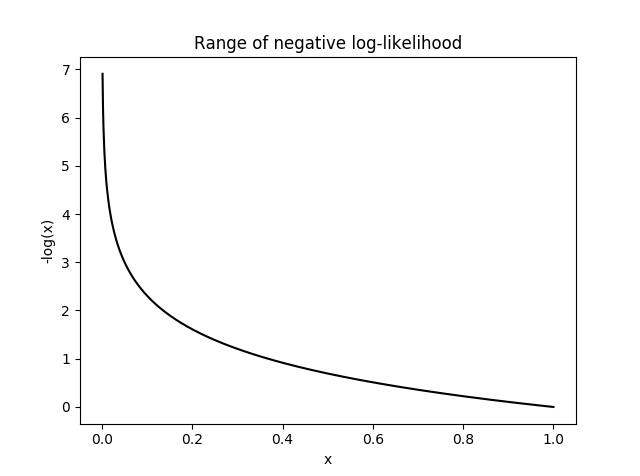
NLL(y)= − log(y)
Combined with softmax, this works to minimize the loss of one hot encoded labels.
Binary Cross Entropy (BCE)
Measures the probability error in discrete classification tasks in which each class is independent and not mutually exclusive. For instance, one could perform multilabel classification where a picture can contain both an elephant and a dog at the same time.
BCE(y)= − y * log(p)−(1 − y)*log(1 − p);y, p ∈ [0, 1]